A CONTRACTING UNIVERSE: AN ALTERNATIVE COSMOLOGY TO ONE OF EXPANSION

By
RUPERT RAYNAR

This paper was written between 1993 and 2011. A shorter version (omitting sections 12 to 15) was published on the internet in 2009. This version was published here in 2012 at:
www.contractinguniverse.co.uk

To contact the author please write to:
Rupert Raynar
16 Killyon Road
South Lambeth
London
SW8 2XT
United Kingdom

Rupert Raynar asserts the moral right to be identified as the author of this work.

DEDICATION: This paper is dedicated to the memory of my uncle, John Raynar, and his wife, Elspeth, who led me to faith in the only Saviour, Jesus Christ, in the summer of 1996

Preface
Abstract

Introduction
The cosmological red shift and a slowing of time
The unchanging speed of light and a contracting universe
A changing mass in a contracting universe
A contracting universe and the force of gravity
The cosmological and gravitational red shifts compared
Paul Dirac's "large numbers hypothesis"
A changing Planck's constant and the light from the distant galaxies
Space as a carrier medium for light and matter
The nature of electric charge in a contracting universe
Magnetic fields as distortions in space
The nature of mass and the fabric of space
The structure of space and quantum uncertainty
Quantum theory's “double-slit” experiment re-examined
Identical parallel universes at different points in their history
Conclusion

References

PREFACE

From the title of this paper, the reader will no doubt have already begun to suspect that any new thoughts or ideas that it may contain might be in complete contrast to the present-day, generally accepted, view that the universe began with the Big Bang some 10 – 20 billion years ago, and has been expanding ever since. Indeed, there will be some who have glanced at the title and decided not even to come this far, for how, in all seriousness, can we be expected to believe in a contracting universe when the evidence has surely pointed for so long to the complete opposite? While the Big Bang model may currently be the best available, I have, however, remained uneasy about the many difficult questions such a theory raises. It is for this reason that, between 1993 and 2011, I tried to construct a different model that would still be in agreement with such evidence as the cosmological red shift. Although my ideas may at first seem strange, I am trusting that the reader will still be tempted to continue, for, starting with just two simple postulates, my hypothesis goes on to describe what I believe to be new ways of looking at the universe, time, space, electromagnetic fields, gravity and quantum mechanics, current theories of which I think need further re-examination if we are ever going to achieve the unification of physics and a combining of relativity with quantum theory.

Rupert Raynar 2011

ABSTRACT

A cosmological model is constructed from two initial postulates. First, that the cosmological red shift can be explained if time everywhere in the universe, and therefore the frequency of light, were slower in the past than it is now. Secondly, that all of nature's constants (e.g., the speed of light, the gravitational and Planck's constant, etc., plus all other entities, e.g., time, distance, mass, energy, charge, force, etc.) should continue to be measured as constant by the inhabitants of the universe throughout all epochs, even though many of them might in fact be changing. It is then argued that, if the measurement of the speed of light remains the same, while the "ticking-rate" of all clocks doubles, going forward in time, the universe, and everything in it, must contract to half its size, along with the wavelength of light. Also, if the measurements of gravity and the electric force are unchanging then mass and charge must halve as the size of the universe halves. Objections that cosmological red shifts would be impossible in a contracting universe are examined alongside gravitational red shifts. It is also shown that, if the universe is a “hypersphere” contracting inwards independently and accelerating then, along with the stretching of space by mass "outwards" in "hyperspace", it might be the cause of gravity rather than the result of it. Thus, in this theory, there is no necessity to invoke the concept of “dark energy” as, unlike in the Big Bang model, there is no need to explain an accelerating expansion of the universe between the galaxies against gravity. Also in our model, there are no problematic singularities, either at the beginning or the end of time. When the age and size of the observable universe is measured in fundamental units, the answer is found to be 1040. Similarly, the electromagnetic force is greater than gravity by the same amount. Paul Dirac proposed, contrary to the accepted Big Bang model, that all three ratios remain equal over time. When applied to our alternative model, not only do they remain equal, but they also remain unchanged at 1040. It is shown too that, for the model to be consistent, all photons, as well as matter particles, must be made from the fabric of space, thereby implying that light is not only a wave in this medium, but both electric and magnetic fields are also distortions in space. The idea is then put forward that an electric field might in fact be due to the twisting of space that occurs when a charged particle is twisted about a higher-dimensional axis. Similarly, magnetic fields are also said to arise from the twisting of space, only in this case the axis is within our own familiar three dimensions. It is also suggested that a particle with mass, results from yet another manifestation of the substance of space: namely, a tiny volume of expanded space or “hump” which protrudes slightly into the fourth dimension of hyperspace. The speculation is made too that space consists of a basic see-through cubic sub-structure of solid elastic interconnecting pathways along which all particles move like solitary waves or “solitons”. It is this fixed structure, through which they travel, that is said to cause particles to follow their uncertain zigzag paths. In addition, each particle is said to be accompanied by a longitudinal wave in the broad overall structure of space that influences which path the particle takes at every junction, though in a probabilistic manner; that is, where the amplitude of the wave is greatest, is where the probability of finding a particle is also greatest. This hypothesis is then used to explain the possible behaviour of the single electrons in quantum theory's famous “double-slit” experiment. Finally, because our universe is said to be a “hypersphere” which is contracting in “hyperspace”, multiple parallel universes may also exist. In addition to that is the idea that all the other universes “inside” and “outside” of ours might be identical in every way, except for their particular point in history.

1. Introduction

In 1929 the astronomer Edwin Hubble made the observation that the spectra of the stars in distant galaxies were shifted to the red end of the spectrum, and that the further away the galaxy, the greater the shift. This momentous discovery has since led many to conclude that the universe must be expanding. The implication of this would seem to be that in the past all the galaxies in the universe must have been closer together, and that if we were to wind the clock back far enough, there would come a time when all the matter in the universe occupied a point of zero volume and infinite density. At such a moment it is said that time and the universe had its beginning, a moment now called the Big Bang.

However, the author of this paper must count himself amongst the few who continue to question this widely accepted model, not least because of the difficulties raised by the idea of a Big Bang singularity. At such a point it would seem that the laws of physics, as we know them, break down. An attempt will therefore be made to outline the main features, albeit very simply, of an entirely different hypothetical model of the universe altogether.

2. The cosmological red shift and a slowing of time

Any theory about the nature of the universe must, of course, agree with observation, not the least significant being Hubble's discovery of the cosmological red shift. In the widely accepted Big Bang model it should be noted that this red shift is said to be caused, not by the galaxies moving away from us through space, but instead by space expanding between the galaxies. The usual analogy is to imagine the galaxies themselves as being represented by dots on a sheet of rubber, which represents space. If the rubber sheet is then pulled outwards, all the dots move away from each other. The light waves from a far-distant galaxy are then said to expand in transit as they travel through this expanding space between that distant galaxy and Earth, thus bringing about the characteristic red shift.

As for this paper's hypothesis, it takes as its starting point two initial postulates. The first is the idea that the cosmological red shift can instead be explained if time everywhere in the universe were slower in the past than it is now. That is to say, all clocks, and therefore the frequency of light, were slower then than they are today. Moreover, the further back in time we go (by examining the light from ever more distant stars), the greater is the slowing down of time and the frequency of light, and hence the greater the red shift. However, in this model, people like ourselves, living long ago near those distant stars, would not have noticed any reddening of the stars' light at all, as the slowing down of the light's frequency would be in keeping with a general slowing down of time.

The second postulate is that all the constants of nature (e.g., the speed of light, the universal gravitational constant, Planck's constant, etc., as well as all other entities such as time, distance, mass, energy, charge, force, etc.) should continue to be measured as constant by the universe's inhabitants throughout all epochs, even though many of them might in fact be changing.

3. The unchanging speed of light and a contracting universe

What then, may one ask, happens to the speed of light? If time is speeding up (that is as we go forward in time), our progressively faster-ticking clocks would gradually measure light as travelling a specific distance, say the radius of an electron, in an ever greater number of "ticks". However, if our hypothetical model is to incorporate the idea, mentioned above, that the measurement of all the constants of nature should continue to remain the same, throughout all epochs, then this constant must be no exception. Thus, for the speed of light to be measured as unchanging, it is necessary that the universe and everything in it contract and become smaller. And so, if there is a doubling of the rate at which all clocks tick, going forward in time, then the size of the universe, along with the wavelength of light, exactly halves. Moreover, the size of everything in the universe also halves: the distance of the Earth to the Sun, the radius of the Earth, the radius of an electron. We can now return to the two-dimensional analogy of the stretched rubber sheet (which represents space), only now it is gradually allowed to contract. This time, however, not only do the dots get closer together, but they also become smaller themselves.

So how might this translate into three dimensions? For reasons that will become clear, if we are going to be able to advance our hypothesis further, then the actual model that should be adopted at this stage is that first suggested by Bernhard Riemann in the nineteenth century. This describes a universe that is finite but unbounded, like the higher-dimensional equivalent of the surface of a sphere. This analogue of a sphere, or "hypersphere", is difficult to imagine, although it can be described mathematically. Using this model, we can extend the analogy of the rubber sheet and say that our hypothetical three-dimensional universe can be likened to the two-dimensional surface of an inflated contracting rubber balloon covered with dots. Thus, as the balloon deflates, the dots become closer together, as well as contracting themselves. Moreover, in the same way that the balloon's contraction causes its surface to move inwards in the third dimension, the universe's contraction as a "hypersphere" causes the fabric of space to move "inwards" in "hyperspace". It is at this point that one can see that the path taken by a body in the space-time of relativity, such as the helix traced out by the orbiting Earth around the Sun, might indeed have an underlying, all-physical reality. For now, as the Earth orbits in three-dimensional space, the fabric of space itself is said to move through a higher physical dimension (hyperspace), thereby tracing out the very same helix described by relativity.

4. A changing mass in a contracting universe

Let us imagine then that, one night while we were all sleeping, the universe and everything in it contracted to half its previous size, in the way we looked at earlier (its mass remaining constant throughout). How would we know the following morning that it had done so? One way would be to examine whether the gravitational force of attraction of the Earth on objects at its surface had altered. From Newton's law of gravitation we can say that the force F between bodies of mass m and M would be given by Equation (1), where d is the distance between them, and G the gravitational constant. (In this case d is the radius of the Earth and M is its mass.)

(1)

Hence, if the radius of the Earth contracted to half its size, the gravitational force, or weight of objects on its surface, would increase by four times. It is here that the author would like to introduce into our hypothetical model the idea of a changing mass, so that as the universe and everything in it halves in size, so does the mass of the universe. Thus, it will be seen that if m and M were to halve while d halves, then F remains completely unaltered. And so it would appear to the universe's inhabitants that everything was remaining the same although size, time and mass were, in fact, all changing. Perhaps one could sum this up by saying: "the more things change, the more they stay the same".

So what does it mean for an object to have mass? A more complete answer than that touched on here, is laid out in section 12, after first considering, in section 9, the idea that matter particles, like photons, might be made out of the substance of space. However, it will suffice here to say, for the sake of our current discussion, that general relativity might point to that quality which enables a body with mass to curve space-time in such a way that the "embedding diagram" for a massive object, such as the Sun, resembles the depression made by a heavy ball placed on a stretched rubber sheet. If this is to be our guide, then let us think of mass in the same way, only in our model the analogy might be with the depression made by a heavy ball in the skin of a contracting balloon, its two-dimensional surface representing three-dimensional space, as we have already seen.

But what, may one ask, actually causes mass to depress the fabric of space in the first place? Before trying to answer this, let us consider at what speed the universe might contract. If anything is to point the way in answering this question, then again it is most likely to be relativity, where events, such as the orbiting of the Earth around the Sun, are viewed in space-time, as we have already mentioned. Thus the orbit of the Earth is not seen as simply a closed ellipse in space, but as a vastly stretched helix in space-time. The degree of stretching is dictated by the speed of light, so that in a single year the "distance" along the time axis is taken as one light year, or approximately 9,500 billion kilometres. With this in mind it seems logical that, in our model, three-dimensional space should contract "inwards" in the higher dimension of hyperspace, at the speed of light. However, while it might indeed be necessary for such a universe to behave in this way, let us consider a possible alternative scenario for reasons that will become clear. Perhaps then we will discover the answer to the above question: how does mass depress space?

5. A contracting universe and the force of gravity

Let us again imagine space as being represented by only two dimensions, namely the surface of a large inflated rubber balloon. In our model, the universe as a hypersphere, one must remember, is contracting inwards in hyperspace, so let us now allow the analogous balloon to contract inwards in the third dimension. As an experiment, let us take the balloon in a space ship far away from the Earth and the effect of the Earth's gravitational field, and observe what happens when we insert a billiard ball inside the contracting balloon. In our first test, let us allow the balloon to deflate at a constant speed, while the ball is touching the inside surface of the balloon. It will be noticed that the ball will move inwards as the balloon contracts, but no stretching of the balloon's skin will take place because the billiard ball is undergoing no acceleration. But what if the balloon contracts at a steadily increasing rate? It will then be observed that, this time, the skin of the balloon is indeed stretched outwards by the ball, and continues to be so, as long as the balloon undergoes this accelerating contraction.

Now let us conduct a further experiment. Let us suppose that a ping-pong ball is introduced into the balloon along with the billiard ball, and again the balloon is allowed to contract at an accelerating rate. Now it will be observed that, if the ping-pong ball is in the vicinity of the billiard ball, the former will be seen to "gravitate" towards the latter as it rolls into the depression. If we now carry over this idea of an increasing rate of contraction to the universe as a hypersphere in our alternative model, it provides a possible way for gravitational attraction to occur. We could therefore sum up by saying that, while there is a case to be made for the speed of contraction of the universe through hyperspace (in our model) to be equal to that of light, there is perhaps a stronger case which suggests that the rate of contraction might be accelerating. By such means gravity might be made possible. Thus it can be seen that Einstein's equivalence principle (that gravity and acceleration are equivalent), is indeed upheld. It might therefore be unnecessary to invoke the exchange of hypothetical "gravitons" between two masses in order to explain this force. Such particles, it has to be said, have never been detected. What, in a sense, we have done is to turn things around and say that space doesn't contract because of the force of gravity between masses occupying space, but that gravity might be explained by an independently contracting space. Put another way, the accelerating contraction of the universe might be the cause of gravity and not the result of it.

Thus far, we have seen how the universe in our model is undergoing, as a hypersphere, an accelerating contraction through hyperspace, while time and mass both change in such a way that the inhabitants of the universe are totally unaware of any change that is going on. Let us now consider what happens as the universe undergoes this contraction. As we have seen, this is said to account for the gravitational attraction between objects with mass. And so, if the universe were to contract in hyperspace with a rate of acceleration that is constant, the acceleration g, experienced by falling objects in the Earth's gravitational field, would always be the same in "real" terms. Thus, if g remained constant, the weight W of an object (or the force exerted on it due to gravity) with mass m, would decline as the universe diminished in size and mass, along with mass m. This can be seen in Equation (2).

(2)

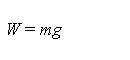
However, since this goes against the idea that the inhabitants of the universe in our model should be unable to measure any fundamental change over time, we might conclude that the rate of acceleration g cannot therefore be constant. Instead, as mass m halves (as the universe halves in size and mass), the rate of accelerating contraction of the universe through hyperspace (and therefore g) must double. By such means the measurement of the quantity W along with mass, g, time, and distance, can remain unchanged for all time.

It is also worth mentioning that, in this cosmological model, (in which the rate of accelerating contraction of the universe as a hypersphere increases over time) there is no need to introduce the concept of "dark energy" which Big Bang adherents have to add to their theory in order to explain the so-called "accelerating expansion" of the universe. Thus, in the Big Bang theory, this strange repulsive force is said to operate in opposition to gravity (and then only between the galaxies) whereas, in our alternative model, gravity is directly and elegantly caused as a result of the accelerating contraction of the universe everywhere.

It is worth pointing out too that, for its inhabitants, as we go forward in time, such a universe would never collapse into a singularity despite diminishing in size at an ever increasing rate. Instead, the measurement of its size would always be the same to its inhabitants ad infinitum. This is due to the fact that its ever faster-ticking clocks would always measure the same number of ticks for a light beam (of unchanging speed) to cross this ever diminishing universe. Even if it were observed from the outside, to one day reach that point of zero size, at the end of time, the maths would still not break down there. This is because the mass of the universe, like distance, would also tend towards zero as that point was approached. In the same way, the length of time between the ticks of the now very fast-ticking clocks would likewise diminish. (Electric charge would, incidentally, behave in a similar manner, as explained later in Section 10.) This is all in complete contrast to the problematic singularity of the Big Bang, where the laws of physics would appear to break down at the moment of creation. One might then wonder, if this is the way the universe behaves as a whole in our alternative model, as it approaches a point of zero size at the end of time, perhaps this then sets the pattern of behaviour for all "black holes" in general, as they also approach similar points in their history. Thus, the maths there too would also stand up. It is thus quite interesting to ponder the idea that, according to our theory, the universe might actually be a giant "black hole" itself.

6. The cosmological and gravitational red shifts compared

Let us return, for a moment, to the matter of the cosmological red shift first noticed by Hubble. In the widely accepted Big Bang model, we have become used to the idea that the light waves from the distant galaxies may supposedly be stretched by an intervening expanding universe. Surely then, if time were slower in the past, as in our hypothetical model, and the light did indeed start out from the galaxies as red-shifted, then if the universe were contracting, might this not result in the light waves being contracted back again on their way to Earth? The result could then possibly be that the latter contraction would cancel out the initial lengthening of the waves, resulting in no red shift at all, or even possibly a blue shift. The answer to this is, it is suggested, to be found by looking at the gravitational red shift. We know that clocks run slower near the surface of a massive object like a star, than they do when further away, in the same way that light from the star is seen as red-shifted by a distant observer, although what exactly is happening is open to argument. The author likes to think of the light waves as having a slower frequency on the surface of the star, which tallies with the overall slowing down of time in that region. Then, as they travel away from the star, they remain unaltered until finally they reach the observer with the same red-shifted frequency with which they began their journey. So what differences are there between the region of space occupied by the star and the distant observer? We know that time goes slower nearer the star and, in accordance with our alternative model of the universe, three-dimensional space is also more stretched nearer the star due to its mass. One can therefore sum up by saying that, as light goes from a more-stretched region of space where time goes slower, to a less-stretched region, where time goes quicker, a red shift occurs. This would appear to have its parallel in the case of the Hubble red shift, in the model of universe we have described. Thus, if one views this hypothetical model (in which the universe contracts), alongside the phenomenon of the gravitational red shift, it should not come as any surprise that light travelling across this contracting universe is, in theory, red-shifted.

7. Paul Dirac's "large numbers hypothesis"

Let us now consider the "large numbers hypothesis" of the physicist, Paul Dirac. A fundamental unit of time, which is sometimes used, is the time that light takes to cross the classical electron radius. If one measures the accepted age of the universe from an assumed Big Bang (approximately 15 billion years), in terms of this fundamental unit, the answer is found to be 1040. It so happens that the electromagnetic force is greater than the force of gravity by the same number 1040. The mystery was why the numbers should be the same. Paul Dirac argued that the number was so large that it was unlikely that the two ratios are equal by coincidence. Furthermore, he maintained that the numbers must be connected by some, as yet unknown, law of nature which requires that they remain equal for all time. So how do we arrive at the age of 15 billion years for the universe in the Big Bang model? We know the distance of the far-away galaxies and, from the Hubble red shift, also their apparent "speed of recession" from us as the universe "expands". Hence, if we reverse this assumed expansion and wind the clock back to the supposed "Big Bang", we can work out its age. However, unlike in the Big Bang model, to the inhabitants of the universe in our alternative model, the distance of galaxies and their Hubble red shift (this time caused by the slowing of time), would continue to be measured as constant (despite the universe's contraction), throughout all epochs. Thus, if the so-called "age" of the universe were to be deduced in the same way as before (that is, by assuming a Big Bang and expanding universe), it would appear always, for all time, to give the same unchanging figure of 15 billion years, or 1040, in the fundamental unit mentioned earlier.

If we were now to think of the universe in the Big Bang model in terms of size instead of age, we can again arrive at the number 1040. This is done by expressing the size of the observable universe in the smallest unit available, the size of an atomic nucleus. In this same model we would again expect this ratio to increase as the universe expanded but, in our alternative model, as the universe halves in size so does the size of an atom, exactly, thus preserving the "magic" number 1040.

8. A changing Planck's constant and the light from the distant galaxies

We have seen how time, distance and mass are all said to vary in our cosmological model in such a way that their measurements continue to remain the same. So what else might vary as the universe contracts, so that its measured value also remains constant? If we take Planck's constant h then we can write Equation (3) where λ is the wavelength of waves associated with particles of momentum p.

(3)

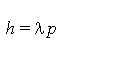
Momentum, in turn, is given by Equation (4) where m is the mass, u the velocity, d is the distance and t is time. Thus we have Equation (5).

(4)

(5)

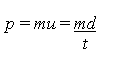
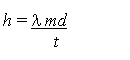
If we were then to turn the clocks back and look at the universe when it was double in size (that is when d was double, m was double, t was double and λ was double) we would see an increase in Planck's constant by a factor of four. (Note: t, or the specific length of time between ticks, would be double, because the clocks would be ticking at half the rate.) So, what would be the energy E of a photon of radiation at such a time, as compared to the energy of a similar photon now? This is given by Equation (6) where v is the frequency.

(6)

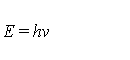
We know that the frequency would be half, along with the rate at which clocks tick. We know also that Planck's constant would be increased four-fold. Thus, from Equation (6), we can say that the energy of all the photons emitted from a star when the universe, and the star, were double in size, would be twice that of the photons emitted from an identical star now, despite being of half the frequency. Now comes the question: if indeed light from a far-distant galaxy began its journey in the form of abnormally energetic photons, what would happen to those photons as they travelled across space and time to us now? Would they remain unchanged and arrive on Earth with all this extra energy in each packet? The answer, it is suggested, lies in the findings of experiments carried out in the 1970s by Baum and Nielson (1976) [1] and Solheim et al. (1976) [2]. Light from nearby galaxies was compared with that from distant galaxies (z = 0.19), and Solheim et al. (1976) concluded that the variation in Planck's constant was less than 5 parts in 1013 per year. Thus, the photons of light reaching us here on Earth from the far-distant galaxies are not abnormally energetic on arrival. However, that doesn't rule out the possibility that they may have had more energy before leaving those distant stars aeons ago. Hence, we might conclude that, if Planck's constant were in fact greater in the distant past, as our alternative cosmological model would suggest, then the energy of those photons might have decreased during their journey across a suggested intervening contracting universe. Now, if we were to ask whether the measured value of Planck's constant here on Earth is currently changing, the answer may come as somewhat of a surprise. It will be remembered (if our model is a correct description of the real world) that the measured value should remain fixed although the constant may in fact be changing. However, yearly measurements of Planck's constant by metrologists here on Earth indicate a value that does vary slightly from year to year, with the graphs, since accurate records began, showing a figure that fluctuates in a way that is not obviously predictable. Thus, an explanation is required for this also, whatever hypothetical model best describes the workings of the universe. However, if we take the results as showing that fluctuations occur around a mean value, that itself does not change, then it is suggested that it is still meaningful to continue with the task of trying to construct a model of the universe that predicts no such measured variation, when considered in its simplest form.

9. Space as a carrier medium for light and matter

Thus, with the results of the 1976 experiments to hand, we might conclude in the case of our model that, as the size of the universe diminishes, so does the energy of all the photons that pass through it (although the frequency with which they began their journey remains unchanged). So how might the energy of a photon be connected with the contraction of space? While our cosmological model as a whole has been constructed from the initial postulate that the Hubble red shift could be explained if time were changing, the author is now going to propose that a photon's energy might vary in the way described, because photons are made out of the fabric of space itself. However, if we were now to ask if the movement of such photons occurred as a wave through this medium, we might expect that the answer would, for most people, be "no", as the idea that there is an "ether" (to use the old-fashioned term) through which light waves travel, "died" as long ago as the first decade of the twentieth century. So what led to its downfall? First of all, instead of the ether's presence being detected by experiment, (most notably that of Michelson and Morley), the speed of light was observed to remain constant for all observers whatever their speed relative to the light source. Secondly, the results of such experiments could be adequately explained by special relativity without recourse to the undetected ether. Thirdly and last of all, the study of electromagnetism by Maxwell seemed to suggest that a changing electric field would cause a changing magnetic field (and vice versa), in such a way that an electromagnetic wave would be able to propagate through space without the need for a carrier medium. Thus, quite reasonably, the idea of space having substance, through which light waves travel, was abandoned; not only could it not be detected, but it did not even need to be invoked in order to explain the behaviour of light. However, it should be noted that, in his paper on special relativity, Einstein does not completely reject the idea of the existence of the ether, but only suggests that it can never be detected. Knowing this, the author feels much happier about suggesting that the notion of space being a carrier medium for light, should be re-examined, although for most people, it is a totally out-dated, rather quaint concept from the nineteenth century that is best left dead and buried.

So henceforth, for the purposes of trying to construct a model that makes some kind of coherent sense, let us say that if photons are made out of space, then since light is also a wave, space must constitute the medium (in our model) through which all electromagnetic vibrations travel. If that were indeed the case, it raises the further possibility that both electric and magnetic fields might be, in effect, some kind of distortion to the fabric of space. This, in turn, would surely point to the need to re-examine other theories, such as quantum electrodynamics. Now the principles of quantum physics tell us that fields should be considered in terms of particles, such that the electric force arises because of the exchange of force-carrying particles between charges; those particles being "virtual photons". However, as their name implies, these "virtual" particles cannot be detected directly, although the success of this theory to date might lead us to believe that we were correct in the supposition that they exist. However, it must also be noted that, from quantum physics, the force of gravity is likely to arise because of the exchange of yet more hypothetical force-carrying particles, in this case "gravitons", between objects with mass. Yet, as we have tried to show, there may be an alternative theory to explain gravity, which does not rely on these so far undetected particles. One might then wonder: if the force of gravity does not need particles to operate, then might not the electric force likewise?

Earlier, bodies with mass were likened to those of billiard balls and ping-pong balls that can move freely across the inner two-dimensional surface of a large rubber balloon; the skin of the balloon representing three-dimensional space. However, it was also stated that, as space contracts (thereby reducing the size of the universe), so do all bodies in space down to the smallest particle. If this is so then it might lead one to conclude that matter particles are not bodies detached from space, as in the balloon analogy above, but are actually, like photons in our hypothesis, made out of the fabric of space also. Perhaps then we would have to acknowledge that, while it may never be possible to detect space, it not only exists but is a medium for matter as well as light. It is here that the author would like to suggest that space consists of a see-through structure made up of solid elastic geometric interconnecting pathways which criss-cross an otherwise empty void. As we shall see later, the suggestion is made that particles might therefore travel through this fixed structure as waves.

10. The nature of electric charge in a contracting universe

At the beginning of this paper, Equation (l) was used to show that as the universe halves in size (along with distance) then so must mass in our model, if the measurement of the force of gravity is to remain constant. By such means, distance, mass and gravity would continue to be measured as staying the same over time. Now we can write an identical equation (see (7) below) for the electrical force F between charges q and Q where C is a constant and d the distance between them. Again, as with gravity, if the measurement of F is to remain unchanged, then as d halves (as the size of the universe halves) so must the charges q and Q.

(7)

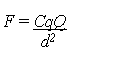
In this way, electric charge (although changing over time like mass, distance and the ticking of clocks) would be measured by the inhabitants of the universe as being constant. Now we can say that the contraction of space is not only accompanied by a reduction in charge, but this hypothesis would appear to be compatible with the, formerly expressed, idea that electric and magnetic fields might be distortions in space as well. At the same time we have the proposition that all matter is made out of space; in which case we might propose that the various ways in which a tiny volume of space might be "knotted-up" into a matter particle, might confer on that particle mass, on the one hand, and charge on the other. Since there must be a connection between a particle's electric field and its charge, the supposed distorted area of space surrounding a charged particle might be due in some part to the way the fabric of space is distorted in the particle itself. While leaving aside, for a moment, how space might confer mass on a particle, the author would, however, now like to propose a mechanism for bestowing charge. First, though, let us remind ourselves that whatever it is that might occur, it must explain how like charges repel, opposite charges attract, and the field around a lone charged particle decreases uniformly in three dimensions. With those "design" considerations in mind, let us return to the idea of three-dimensional space being represented by the two-dimensional surface of a balloon, and suggest that, if a particle is represented by a spot on the balloon, then its charge is analogous to the twisting of that spot about the third-dimensional axis that passes through it and the centre of the balloon. This, in turn, would cause an outwardly spreading, uniformly decreasing, twisting of the balloon's two-dimensional surface away from the twisted central spot. Not only that, but in the same way that this occurred about the spot's third-dimensional axis, when translated to the universe in our model, a charged particle could be described as a point in space that was twisted about a higher-dimensional axis. Furthermore, it is proposed that it is the direction of twist (clockwise or anti-clockwise) that gives rise to either a positive or negative charge, while the amount of charge is arrived at by the degree of twist. Now it is easy to see that, if particles were made out of space as suggested, and their charge were due to this twisting, then the space surrounding the particle would also be twisted, as in the balloon analogy. What is more, we could speculate that the force that arises between two charged particles is due to the interaction of their two areas of twisted space (the fields), and that each particle "feels" this force since it is connected, in essence, to its field by a real physical substance, i.e., space.

11. Magnetic fields as distortions in space

As we have seen, in our cosmological model light waves are said to be waves in the fabric of space, thereby implying that both electric and magnetic fields might be distortions of some kind in that same medium. This then led us to consider the nature of electric fields in this alternative model. However, that leaves us with one more question: how might magnetic fields arise in a way that is consistent with our overall hypothesis? An answer to this is as follows:

Earlier, it was proposed that electric fields might result from the twisting of space, albeit around a higher-dimensional axis. The author would now like to suggest that magnetic fields occur in a similar way, only this time the twisting takes place around an axis in our own familiar three dimensions of space. By way of illustration, let us take a simple bar magnet. In this case the axis is said to run through the length of the magnet from end to end, so that if we were to look head-on at, say, the north pole, we would see the surrounding fabric of space twisted in perhaps a clockwise direction. Similarly, when examining the south pole head-on, the direction of twist would be anti-clockwise. Thus, as we saw in the case of electric charges, when two magnetic poles are brought together, a force is said to result from the combining of each area of twisted space.

12. The nature of mass and the fabric of space

So far, we have seen how bodies with mass are said to cause three-dimensional space to be stretched "outwards" in hyperspace as the universe contracts, while those same bodies are said to be made from the substance of space itself. At the same time, we have conjured with the idea that, as the universe, and thereby space, diminishes, so does the size of all bodies in space, as well as their mass, in equal proportions. If the size of the universe halves then the size and mass of every body in the universe also halves, exactly. Clearly then, for our cosmological model to work, there must be a mechanism directly linking mass with the fabric of space such that, as space shrinks, so does mass. Let us therefore return to the idea that the universe is a hypersphere and that three-dimensional space can be represented by the two-dimensional surface of a balloon. It is here that the author would now like to suggest that a particle with mass is simply a tiny area of stretched space which produces a small "hump" in the surface of the balloon. (That is when viewed from the outside.) Thus, in this analogy, the two-dimensional surface of the "hump" protrudes slightly into the third dimension surrounding the balloon. Hence, in our cosmological model, a particle with mass can be said to be a tiny volume of expanded space which produces a three-dimensional "hump" that extends slightly into the fourth dimension of hyperspace. It can therefore also be said that this notion of mass is compatible with our idea that massive bodies also "depress" space "outwards" in hyperspace as the universe undergoes its accelerating contraction, thereby producing gravity. We can also add that the larger the "hump", the greater the mass. Thus, as the universe contracts over time, and space diminishes, so do the "humps", and therefore so do all the masses produced by the "humps". Also, it is easy to see how such entities might "ripple" through the fabric of space, as they travel like waves through that solid elastic geometric structure of pathways suggested earlier.

13. The structure of space and quantum uncertainty

Towards the end of the previous section, the idea was reiterated that space might consist of interconnecting pathways. The author would now like to develop this hypothesis further, and suggest that it may go some way towards providing an explanation for some of the uncertainties in quantum theory. For, if particles were all constrained to following certain physical pathways through space then, instead of travelling in straight lines, they would have to zigzag their way through this fixed geometrical structure. To illustrate what might happen, let us therefore carry out the following very basic thought experiment as we put forward a very simple representation of space should it exist in only two dimensions. Later, we will go on to provide a possible tentative theory to explain how particles might travel across space in our real three-dimensional world.

So, let us begin by erecting a vertical two-dimensional "honeycomb" structure of interconnecting tubes (representing space) through which closely-fitting ball bearings (representing particles) can travel down under gravity. Also, to make things simple, let this "honeycomb" structure be held in exact "vertical alignment". Then, let us place one ball bearing after another into one of the ends of the tubes at the top of the structure, and observe what happens. The balls would follow a zigzag path, under gravity, all the way to the bottom, with most of the balls ending up at a point directly below their above starting position. This is because, when the balls arrive at every other junction in the "honeycomb" structure of tubes, on their way down, there is an equal probability that the balls will go to the left as well as to the right. However, a smaller number of balls would, in all probability, go to the left, say, more often than they would go to the right (and vice versa) as they continued to travel. Thus, in time, all the balls at the bottom of the structure would be spread out after their journey, with most in the middle, then progressively fewer the greater the distance from the centre. It is in such a similar way that the suggestion is made that all particles move through space. Thus, in all probability, most would, most of the time, move close to a straight line, although a smaller number would, nonetheless, deviate from it. Hence, to conclude, the uncertain zigzag paths taken by every particle moving through space (and hence also the particles' uncertain positions at any one moment) are said to arise because of the probabilities that are introduced at every junction of space's fixed geometrical structure. In such a way, this may, in part, explain where some of the uncertainties and probabilities of quantum theory originate from.

Now let us look at how particles might behave in the real world as they travel across a three-dimensional space. Let us also keep to the idea that space has structure although what form it might take might arguably be quite different in three dimensions compared to that of the two-dimensional "honeycomb" we have just been considering. With that in mind, the author would like to propose that the basic building-block of three-dimensional space is the "cube", as this is the only regular space-filling polyhedron which can produce a tiling of 3-D Euclidean space, when all the tiles are identical. Thus, a two-dimensional cross-section of this said space would resemble a sheet of squared graph paper with equidistant horizontal parallel lines crossing identical vertical lines at 90º. Particles, it is suggested, are then said to travel along these lines or pathways as solitary waves or "solitons". As we saw earlier, the movement of such particles is compatible with the idea that those with mass might be small three-dimensional "humps" of expanded space that slightly protrude into hyperspace.

The next thing to point out is that, unlike in our earlier thought experiment (where the ball bearings and regular hexagons were of a similar size), the actual dimensions of the basic cubic sub-structure of space are likely to be many times smaller than the smallest particle. When we consider that the Planck length is some twenty powers of ten below the diameter of a proton this is easily possible. This would mean that, when particles collide (from whichever direction), they are able to make contact with each other at the appropriate angle, whatever that is, despite being restricted to 90º zigzag movements at a smaller fundamental level. However, this is far from being the whole story as we shall see. There remains the question of how particles might retain their momentum and exact overall direction of travel (after, say, a collision with another particle) while still being constrained, at the same time, by the fixed structure of pathways they are forced to inhabit.

It is here that the author would now like to suggest that, in addition to particles having a definite identity and mass, (while moving at speed through space as a solitary wave or soliton) their direction of travel, and the paths they are most likely to take at every junction they come to, are governed by yet another wave. This time it is a "longitudinal" or "pressure" wave (like that of sound) which is said to propagate (unlike the solitary wave of each individual particle which is constrained to the pathways) through the broad, overall structure of space. Thus, when a force is applied to a particle, thereby giving it a definite velocity and momentum, at that same moment the longitudinal wave is said to begin to propagate through space with exactly the same speed and direction as was imparted to the particle by the force. If we now introduce the idea that the particle (travelling at the same speed and within the same vicinity as the longitudinal wave) is more likely to choose at every junction in the fabric of space which it comes to, the path where the amplitude of the longitudinal wave is greatest, then the following may be seen to occur: namely, the particle will tend to travel over time in the same direction as the longitudinal wave, while also moving in an uncertain zigzag manner through the three-dimensional cubic sub-structure of space suggested earlier. Hence, the probabilistic paths taken by our particle will tend to mimic, in a similar way, those of the ball bearings in our previous two-dimensional thought experiment. Thus, the broad-front longitudinal wave through the fabric of space, in our theory, can be said to be both a real physical wave in a real physical substance, as well as being a measure of probability, so that where the wave's amplitude is greatest, is where the probability of finding a particle is also greatest.

14. Quantum theory's "double-slit" experiment re-examined

As we have been seeing, perhaps our picture of what might be going on at a quantum level can offer some fresh insight into one of quantum theory's most defining of all experiments, that of the "double slits". This was first done by Thomas Young in England in the early nineteenth century using monochromatic light, but has since been repeated using electrons. However, a deeply puzzling thing happens when only single electrons pass through the apparatus. In the experiment, (which has the same outcome if single photons are used) these single electrons are fired, one at a time, from an electron gun, towards two narrow adjacent parallel slits in a nearby screen. Then, having passed through one or other of the slits, the presence of each electron is finally recorded as they arrive, one after the other, at a final detector screen. There, spots of light are produced on the screen (say a phosphorescent one like that in a cathode ray tube television) as the electrons strike, while the cumulative build-up over time is recorded, say, on video. However, the pattern which emerges across the final screen (and this is the puzzle), after many individual electron hits, resembles the light and dark interference bands which Young first witnessed in his similar experiment using a monochromatic light source. Now we know how to explain the pattern in the case of the latter, in terms of light being a wave. Thus, after the light from the initial narrow source in Young's experiment has reached the two slits, it is diffracted and the two spreading "wavelets" that emerge, propagate independently of each other while still retaining the same wavelength. They then proceed towards the final screen where, like any wave system, interference between them takes place as they come together. It is there that, (the waves being of the same wavelength) if they overlap in-step, they reinforce each other and a bright band results. Similarly, when they are out-of-step and the waves cancel there is the absence of a bright band. We should also note that such interference "fringes" only occur (for both light and the single electrons) when both slits are kept open.

So, to recap, it would seem that, even though a wave-like interference pattern appears over time on the final screen when single electrons are used, they should logically pass alone through only one slit. Similarly, they again behave like single particles when they strike the final screen in just one place on arrival. So, how then can they "know" of the existence of the other open slit so that over time the interference pattern on the final screen is built up? The situation becomes yet more confusing when we keep both slits open but use a detector to determine through which slit each electron passes. In that event the electrons still arrive at the final screen like before, but this time without causing the build-up of the interference pattern. This then raises the question of how can merely measuring an electron's state in-transit affect the final outcome. Hence, it might appear that each electron "knows" both whether or not the two slits are open, as well as whether or not it is being observed, and adjusts its behaviour accordingly. If we watch it, the electron behaves like a particle; if we don't, it behaves like a wave. We are thus left with a puzzle which theorists of current quantum mechanics, although accepting and being able to usefully quantify mathematically, are nonetheless unable to adequately explain. So can our tentative theory possibly offer any new insights into this seemingly intractable problem in physics? The answer, it is suggested, may be "yes" as we shall see.

First, let us consider the passage of the single electrons through the experimental apparatus while not being observed; that is, without there being a device to detect through which of the two slits each electron passes. Now, we might suspect, from the build-up of the interference pattern across the final screen over time, that a wave of some kind passes through both open slits. However, at the same time, each electron (being a particle) can also logically be said to pass through only one of the two slits. Now, it might at first appear that such a wave-particle duality cannot be adequately explained. However, if we apply our theory and suggest that space has structure and that two different waves (solitary and longitudinal) are involved in the movement of the electrons, then a clearer picture begins to unfold. Thus, while each electron as a solitary wave is said to pass through only one slit, the associated broad-front longitudinal wave that accompanies it, (which travels at the same speed as the electron all the way from its initial source, the electron gun) can be said to pass through both slits. This longitudinal wave then behaves like any wave, such that, after being diffracted at the two slits, the two emerging coherent "wavelets" (each of the same wavelength in this case) proceed towards the final screen where interference between them takes place. Now, according to our theory, where the amplitude of the longitudinal wave is greatest, is where the probability of finding an electron is also greatest. Hence, where the interference at the screen causes an overlapping in-phase of the two wavelets (and thereby a combined increased amplitude) right there, is the electron most likely to be found. Conversely, where the wavelets cancel, due to overlapping that is out-of-phase, the combined amplitude will be a minimum and therefore the chances of finding an electron there also a minimum. Hence, over time (as the experiment is repeated) the characteristic alternating bright and dark interference bands will accumulate across the screen.

Now let us re-run the experiment with a detector at the slits to observe through which of them each electron passes. This time, the cumulative image of the electron strikes on the final screen shows no signs of an interference pattern. So how can this be? First, let us recall that, according to our theory, the electron travels from its initial source (the electron gun) together with its associated broad-front longitudinal wave towards the two slits where, as a particle, it then passes through just one of them. However, if we detect the electron at either slit, however subtly, such measurement nevertheless slightly alters its momentum. It is this that is then said to cause a change in the wavelength of the longitudinal wave at that particular slit. This, in turn, would mean that the two wavelets, emanating from the two slits, would no longer share the same wavelength unlike before, when there were no detectors at the slits and they were created from the same single undisturbed broad-front longitudinal wave. Now, the wavelets must share the same wavelength if they are to cohere and overlap either in-phase or out-of-phase at the final screen. If they do not (as is the case here) then there will be no alternating areas of increased and decreased probability of finding an electron (caused by the increased and decreased amplitude of the combined longitudinal wavelets) and therefore no bright and dark interference pattern over time across the screen.

We have thus, using our theory of the two waves and the cubic sub-structure of space, been able to suggest, at least in part, how electrons might behave at the quantum level both as particles and also as waves, while acting, at the same time, in the same uncertain and probabilistic manner described by conventional quantum theory.

15. Identical parallel universes at different points in their history

Finally, the author would like to speculate further on the idea (expressed earlier) that the universe in our model is a hypersphere which is contracting in hyperspace. Thus, parallel universes, both "inside" and "outside" of our own particular universe, may also exist. This concept is not new, of course, although we might add to it the suggestion that all of them, right down to the position and momentum of every particle, may be identical to ours in every way, except for their particular point in history. Thus, those on the "outside" are said to be exact snapshots (though just as real as ours) of what our universe was like in the past; while those on the "inside" are exact representations of what our universe (and everything in it) will become in the future. If this were so, it would surely lead to such interesting questions as whether it would ever be possible for information (maybe at a quantum level) to travel between these separate, but yet related, universes.

16. Conclusion

Looking back at what is only the outline of a possible alternative theory to that of the widely accepted Big Bang model, it becomes clear that there is much we have not considered. For instance how, in such a contracting universe, might it be possible for the measurement of the remaining forces, along with gravity and electromagnetism, to remain unchanged over time, together with the measured values of all the other entities and constants of nature? Many questions would therefore need to be answered before this, very different, theory started to take shape.

Summing up, then: the hypothetical model of the universe here described would appear to be far removed from the model we are all used to. Instead of the cosmological red shift being caused by the expansion of space, it results from a slowing of time; and instead of the universe expanding between the galaxies, it contracts everywhere, while time, mass and electric charge change with it. Not only that, but this takes place while the measurement of all such entities and constants of nature remains the same to the inhabitants of the universe throughout all epochs. Also, gravity is caused by the accelerating contraction of the universe as a "hypersphere", and not by hypothetical gravitons. In addition, there are now no problematic singularities, either at the beginning or end of time. Neither does "dark energy" need to be invoked in order to explain any aspect of this universe, unlike in the Big Bang model. Even the commonly held idea that parallel universes might exist "inside" and "outside" of our own, has been enlarged on further, with the additional suggestion that they might all be identical to ours in every way, except for their particular point in history. But perhaps the most dominant underlying hypothesis, drawing everything together in this wide-reaching paper, is the idea that space is a real physical substance, and that all the distinct entities of mass, charge, light, forces and fields, although appearing to exist in a universe where there is no carrier medium, are instead all manifestations of that single substance and the way it behaves. Thus, particles with mass were said to be "humps", while those with charge were "twists" within that same fabric. Finally, after suggesting a possible see-through elastic cubic sub-structure for space, as well as the two different waves by which particles are able to zigzag their way through its interconnecting pathways in a probabilistic manner, we saw how it might explain the wave-particle duality of electrons, as well as their behaviour in quantum theory’s famous "double-slit" experiment.

In 1916 Einstein published his general theory of relativity, although he initially found it difficult to accept some of the implications of the theory, as it seemed to be saying that the universe was a changing and dynamic place. Hitherto, and for some time afterwards, he stuck to the idea that the universe was static, so much so that he introduced a cosmological constant into his theory so that it would agree with his beliefs. He later described it as the biggest blunder of his life. Yet, when I think of this, I wonder whether he was not right on both counts. To us, who inhabit the universe, I believe it does appear to be static while, by what might seem a strange paradox, the universe is indeed, as general relativity predicts, a place of change. What the surprise might be to all of us is that the universe may be far more dynamic than we might have hitherto imagined!

References

[1] W.A. Baum and R. Florentin-Nielson, "Cosmological Evidence Against Time Variation of the Fundamental Atomic Constants", Astrophysical Journal, 1976, Vol. 209, pp. 319-329.

[2] J.E. Solheim, T.G. Barnes III and H.J. Smith, "Observational Evidence Against a Time Variation in Planck's Constant", Astrophysical Journal, 1976, Vol. 209, pp. 330-334.

Download this document as PDF